Lucene打分公式的数学推导
在进行Lucene的搜索过程解析之前,有必要单独的一张把Lucene score公式的推导,各部分的意义阐述一下。因为Lucene的搜索过程,很重要的一个步骤就是逐步的计算各部分的分数。
Lucene的打分公式非常复杂,如下: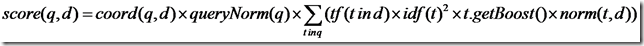
- t:Term,这里的Term是指包含域信息的Term,也即
title:hello和content:hello是不同的Term - coord(q,d):一次搜索可能包含多个搜索词,而一篇文档中也可能包含多个搜索词,此项表示,当一篇文档中包含的搜索词越多,则此文档则打分越高。
queryNorm(q):计算每个查询条目的方差和,此值并不影响排序,而仅仅使得不同的query之间的分数可以比较。其公式如下:
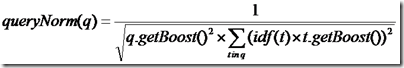
tf(t in d):Term t在文档d中出现的词频
- idf(t):Term t在几篇文档中出现过
norm(t, d):标准化因子,它包括三个参数:
- Document boost:此值越大,说明此文档越重要。
- Field boost:此域越大,说明此域越重要。
- lengthNorm(field) = (1.0 / Math.sqrt(numTerms)):一个域中包含的Term总数越多,也即文档越长,此值越小,文档越短,此值越大。

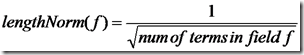
各类Boost值
- t.getBoost():查询语句中每个词的权重,可以在查询中设定某个词更加重要,
common^4 hello - d.getBoost():文档权重,在索引阶段写入nrm文件,表明某些文档比其他文档更重要。
- f.getBoost():域的权重,在索引阶段写入nrm文件,表明某些域比其他的域更重要。
以上在Lucene的文档中已经详细提到,并在很多文章中也被阐述过,如何调整上面的各部分,以影响文档的打分,请参考有关Lucene的问题(4):影响Lucene对文档打分的四种方式一文。
- t.getBoost():查询语句中每个词的权重,可以在查询中设定某个词更加重要,
然而上面各部分为什么要这样计算在一起呢?这么复杂的公式是怎么得出来的呢?下面我们来推导。
首先,将以上各部分代入score(q, d)公式,将得到一个非常复杂的公式,让我们忽略所有的boost,因为这些属于人为的调整,也省略coord,这和公式所要表达的原理无关。得到下面的公式:
然后,有Lucene学习总结之一:全文检索的基本原理中的描述我们知道,Lucene的打分机制是采用向量空间模型的:
我们把文档看作一系列词(Term),每一个词(Term)都有一个权重(Term weight),不同的词(Term)根据自己在文档中的权重来影响文档相关性的打分计算。
于是我们把所有此文档中词(term)的权重(term weight) 看作一个向量。
Document = {term1, term2, …… ,term N}
Document Vector = {weight1, weight2, …… ,weight N}
同样我们把查询语句看作一个简单的文档,也用向量来表示。
Query = {term1, term 2, …… , term N}
Query Vector = {weight1, weight2, …… , weight N}
我们把所有搜索出的文档向量及查询向量放到一个N维空间中,每个词(term)是一维。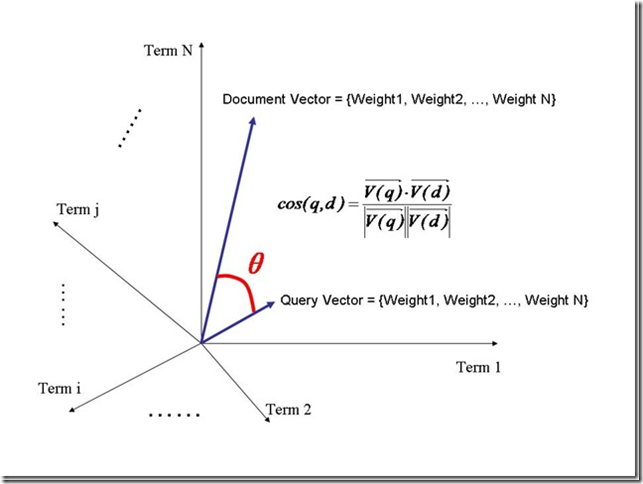
我们认为两个向量之间的夹角越小,相关性越大。
所以我们计算夹角的余弦值作为相关性的打分,夹角越小,余弦值越大,打分越高,相关性越大。
余弦公式如下: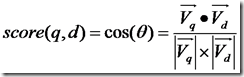
下面我们假设:
查询向量为Vq =
文档向量为Vd =
向量空间维数为n,是查询语句和文档的并集的长度,当某个Term不在查询语句中出现的时候,w(t, q)为零,当某个Term不在文档中出现的时候,w(t, d)为零。
w代表weight,计算公式一般为tf*idf。
我们首先计算余弦公式的分子部分,也即两个向量的点积:
Vq*Vd = w(t1, q)*w(t1, d) + w(t2, q)*w(t2, d) + …… + w(tn ,q)*w(tn, d)
把w的公式代入,则为
Vq*Vd = tf(t1, q)*idf(t1, q)*tf(t1, d)*idf(t1, d) + tf(t2, q)*idf(t2, q)*tf(t2, d)*idf(t2, d) + …… + tf(tn ,q)*idf(tn, q)*tf(tn, d)*idf(tn, d)
在这里有三点需要指出:
- 由于是点积,则此处的t1, t2, ……, tn只有查询语句和文档的并集有非零值,只在查询语句出现的或只在文档中出现的Term的项的值为零。
- 在查询的时候,很少有人会在查询语句中输入同样的词,因而可以假设
tf(t, q)都为1 - idf是指Term在多少篇文档中出现过,其中也包括查询语句这篇小文档,因而
idf(t, q)和idf(t, d)其实是一样的,是索引中的文档总数加一,当索引中的文档总数足够大的时候,查询语句这篇小文档可以忽略,因而可以假设idf(t, q) = idf(t, d) = idf(t)
基于上述三点,点积公式为:
VqVd = tf(t1, d) idf(t1) idf(t1) + tf(t2, d) idf(t2) idf(t2) + …… + tf(tn, d) idf(tn) * idf(tn)
所以余弦公式变为: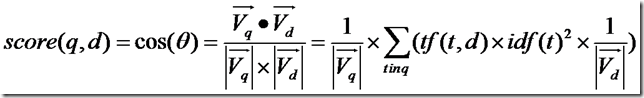
下面要推导的就是查询语句的长度了。
由上面的讨论,查询语句中tf都为1,idf都忽略查询语句这篇小文档,得到如下公式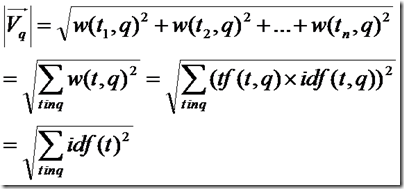
所以余弦公式变为:
下面推导的就是文档的长度了,本来文档长度的公式应该如下: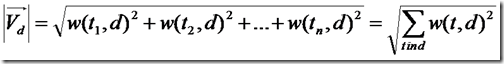
这里需要讨论的是,为什么在打分过程中,需要除以文档的长度呢?
因为在索引中,不同的文档长度不一样,很显然,对于任意一个term,在长的文档中的tf要大的多,因而分数也越高,这样对小的文档不公平,举一个极端的例子,在一篇1000万个词的鸿篇巨著中,”lucene”这个词出现了11次,而在一篇12个词的短小文档中,”lucene”这个词出现了10次,如果不考虑长度在内,当然鸿篇巨著应该分数更高,然而显然这篇小文档才是真正关注”lucene”的。
然而如果按照标准的余弦计算公式,完全消除文档长度的影响,则又对长文档不公平(毕竟它是包含了更多的信息),偏向于首先返回短小的文档的,这样在实际应用中使得搜索结果很难看。
所以在Lucene中,Similarity的lengthNorm接口是开放出来,用户可以根据自己应用的需要,改写lengthNorm的计算公式。比如我想做一个经济学论文的搜索系统,经过一定时间的调研,发现大多数的经济学论文的长度在8000到10000词,因而lengthNorm的公式应该是一个倒抛物线型的,8000到 10000词的论文分数最高,更短或更长的分数都应该偏低,方能够返回给用户最好的数据。
在默认状况下,Lucene采用DefaultSimilarity,认为在计算文档的向量长度的时候,每个Term的权重就不再考虑在内了,而是全部为一。
而从Term的定义我们可以知道,Term是包含域信息的,也即title:hello和content:hello是不同的Term,也即一个Term只可能在文档中的一个域中出现。
所以文档长度的公式为: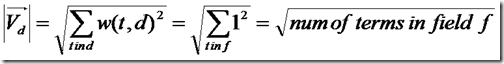
代入余弦公式: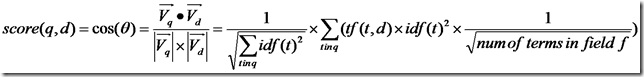
再加上各种boost和coord,则可得出Lucene的打分计算公式。

